En el proceso de planificación de un proyecto, es fundamental calcular el tiempo necesario para su realización. Dado que un proyecto consta de múltiples tareas, la planificación temporal del conjunto del proyecto se relaciona directamente con la estimación del tiempo necesario para realizar cada una de las tareas.

¿Quién debe estimar la duración de una tarea?

Deben hacerlo personas que estén acostumbradas a ejecutar tareas similares a la que se desea estimar. Ellas entenderán la complejidad de la tarea y por tanto el tiempo que se necesita para completarla. Del mismo modo, de cara a una estimación del presupuesto o de los recursos humanos necesarios, una opinión de un experto en ese ámbito puede aportar mayor seguridad y precisión en la planificación de la tarea. Sin embargo, cualquier estudio debe apoyarse en la mayor solvencia matemática posible.

¿Cómo se estima la duración de una tarea?

Existen diferentes métodos en función de los riesgos asociados y de la variabilidad intrínseca a la tarea. Conviene diferenciar bien estos dos conceptos. Los riesgos deben incluirse en el apartado de gestión de riesgos, y no deben considerarse en la estimación de la duración de la tarea ni incluirse en el cronograma.

En este apartado, debemos centrarnos en la estimación temporal que tiene en cuenta los factores de variabilidad que son inherentes a la tarea y que no se pueden evitar, por lo que se deben incluir en el cronograma.

Como en cualquier estimación, existe un valor central o medio y un rango o intervalo de confianza, para el que se debe aportar un porcentaje de certeza.

Hay diferentes métodos de estimación:

Estimación por analogía:

Consiste en estimar la duración de una tarea a partir de los datos históricos disponibles. Para ello, será necesario recopilar trabajos similares al que queremos estimar que hayan sido previamente realizados por nuestra empresa o por otras. Conociendo sus tiempos de ejecución, podemos obtener estadísticos descriptivos, como la media del tiempo de realización o la desviación estándar de este parámetro. Asumiendo que la duración de estos proyectos siga una distribución normal o gaussiana, podemos establecer intervalos de confianza. Por tanto:

• La media +/- una desviación estándar, estimará un intervalo de confianza del 68%.
• La media +/- 2 veces la desviación estándar, calculará un intervalo de confianza de un 95%.
• La media +/- 3 desviaciones estándar, establecerá una probabilidad de un 99%.

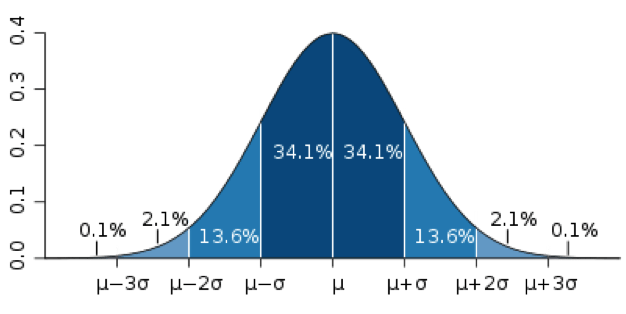
La recopilación de más estudios, permitirá realizar una estimación más exacta tanto de la media como de la desviación estándar.

Al mismo tiempo, como se puede observar, conseguir intervalos de confianza con un elevado porcentaje de acierto implicará que el parámetro estimado tendrá una mayor variabilidad. Observando la gráfica de la campana de Gauss, se puede intuir que, en los valores centrales, incluir pequeñas variaciones en la suma/resta de desviaciones típicas implica gran rendimiento en cuanto a porcentaje de acierto de la estimación. Sin embargo, en los extremos de la curva, es necesario incluir mucha variación en las desviaciones típicas para apenas incrementar el grado de certeza de la estimación. Por ello, en la mayoría de los trabajos, se realizan estudios con un intervalo de confianza del 95%, es decir, la media +/- 2 desviaciones estándar. Es el valor consensuado para el cual se consigue un mayor grado de confianza con una menor variabilidad del parámetro estimado.

Aunque la distribución normal es aquella que obtendremos en la mayoría de los estudios (y de las variables naturales), en ocasiones, los trabajos recopilados mostrarán una duración de las tareas que se ajustará más a una distribución normal logarítmica. En estos casos, la curva de distribución se caracteriza por mostrar un comportamiento gaussiano para valores bajos, mostrando un comportamiento logarítmico para valores más altos. Esto significa que existen grupos de trabajo que muestran unos tiempos de ejecución anormalmente altos.

En estos casos, no tiene sentido el cálculo de valores medios y desviaciones típicas incluyendo todos los trabajos. Solamente deberán incluirse aquellos que no muestren unos tiempos de ejecución anormalmente altos. Los trabajos que “se salen de lo normal”, también deben ser estudiados, pero de otra manera. Debemos centrarnos en buscar factores externos que hayan alterado su ejecución, de los que también debemos estar informados.

Otra posibilidad es que el alcance de esos proyectos sea mucho mayor que el del resto de trabajos que estamos estudiando. Si todos los proyectos analizados tienen una escala local y uno de ellos tiene una alcance internacional, es probable que este último necesite un tiempo de ejecución muy superior. En casos como éste último, sería más interesante realizar una aproximación paramétrica.

Estimación paramétrica:

Es una técnica de estimación muy similar a la estimación por analogía, pero en este caso no se dispone de trabajos previos con un alcance similar al que queremos desempeñar. La solución es utilizar factores de corrección que tengan en cuenta la magnitud del proyecto. Para ello, la técnica matemática que se utiliza es la regresión lineal.

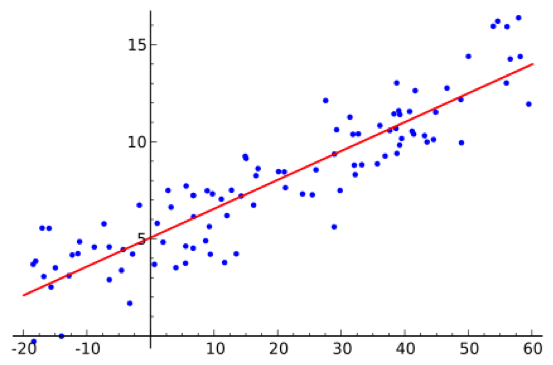
Por ejemplo, si se ha ejecutado un proyecto a escala nacional en países de pequeña población y de gran población, sin existir países medianos (el ámbito en el que deseamos llevar a cabo nuestro proyecto), se debe realizar una estimación para los trabajos realizados en países pequeños y otra diferente para los países grandes. Posteriormente, se deberá calcular un factor de corrección en función del número de habitantes. Así, por interpolación se podrá calcular el tiempo necesario para la realización del proyecto en un país de un tamaño intermedio.

Otro factor que se debe tener en cuenta es la curva de aprendizaje. Si un proyecto debe realizarse repetidamente, es evidente que cuantas más repeticiones, más rápida será su ejecución. Por ello, si todos los datos que extraemos proceden de grupos experimentados, la estimación realizada no será realista. Será necesario incluir factores de corrección que tengan en cuenta el número de repeticiones y la curva de aprendizaje.

Estimación por criterio de expertos:

Es la menos recomendable, pero en algunas ocasiones es la única disponible (como en casos de falta de datos históricos o de existencia de mucha disparidad entre éstos). También debe tenerse en cuenta que, aunque las demás técnicas expuestas son matemáticas, sigue siendo necesaria la intervención humana para considerar los trabajos previos que se deben incluir y el modelo matemático a aplicar. Por tanto, la realización de cualquier tipo de estudio por parte de expertos implica cierta garantía.

Una manera de mejorar esta estimación consiste en acudir a varios expertos de manera independiente. Posteriormente se podrán promediar los resultados propuestos por cada experto y así intentar obtener una visión más global y menos sesgada por los criterios particulares de cada uno de ellos.

Otra manera de mejorar la estimación realizada por este último método es lo que se conoce como la estimación por tres puntos. En estos casos, se les pide a los expertos que realicen una estimación media, una estimación pesimista y estimación optimista. Posteriormente, se obtendrán resultados promedio de estas tres estimaciones.

Como cualquier sistema, este también tiene sus defectos. Las estimaciones pesimistas y optimistas pueden tener en cuenta riesgos externos, que no deberían incluirse en la estimación de la duración de una tarea. Será, por tanto, tarea del director de proyectos dilucidar estos puntos y poder facilitar una estimación más precisa. De todas formas, como se ha explicado anteriormente, estos últimos métodos se basan fundamentalmente en el criterio humano, por lo que están más sujetos a error que otros métodos fundamentados en el análisis matemático.